摘要 为满足人体关节运动模型研究的需要，设计了一种基于机器视觉的肢体运动模式采集系统，系统由PCI-1411视频采集卡和LabVIEW数字图像处理平台构成。通过对采集到的肢体运动状态视频分帧进行处理，建立了肢体关节运动的相关数学模型，获得了较为准确的肢体运动参数。研究结果表明，采用视频采集技术建立的运动模型较传感器采集技术建立的模型有精确度高、处理速度快、系统误差小、数据易分析处理等优势。
关键词 视频采集；LabVIEW；数字图像处理；肢体运动模型

    肢体运动过程的研究是运动学、生命科学、自动控制等学科的重要研究对象，最典型的应用是机器人研究，其成果可应用于人体假肢的设计等多个方面。而目前的假肢设计技术，使得产品价格昂贵、控制复杂，无法满足广大残障人士的需求。要改善肢体残障人士的生存状况，促进假肢设计与制作技术的发展，研究出结构简单、步态逼真、成本低廉的假肢，具有重要的现实意义，肢体运动模型的建立是假肢设计中关键的研究内容。
    传统肢体运动过程的研究一直沿用各种机械模拟和数字转换装置做模型采集系统，这种系统因大量数据采集和处理任务所带来的系统误差导致了模型失真较大。随着信息技术的发展，视频采集和数字图像处理技术因其采集方便、处理速度快、精度高而被应用到各种测控领域。在众多的视频采集处理方案中，美国国家仪器公司的视频采集卡PCI-1411及LabVIEW处理平台，具有强大视频采集和数据处理能力。应用该开发平台设计的视频采集系统建立肢体运动模型研究，是以人类下肢运动过程为对象，在脚尖末梢、踝关节、膝关节及大腿末端关节处安装LED点光源，可以精确采集到各肢节的运动轨迹，从而建立完整的肢体运动过程模型。其基本原理为通过摄像头实时采集固定在肢体关节处的点光源运动序列，使用数字图像处理技术和视频连接技术，描绘出肢体的运动轨迹棍状图。通过对光点进行坐标量化，构造出肢体运动模型。对运动模型应用数学几何测量的知识，获得肢体运动的模型参数，建立出肢体运动的数学模型。

1 肢体运动模型采集系统的构建
    应用视频采集的方法构建的肢体运动模型采集系统，由视频获取装置和视频处理软件两部分构成。视频获取装置包括点光源、摄像机、视频采集卡和PC机。点光源使用1 W红色LED，将其固定在肢体关节处，摄像机采用Timber2038型行间变换CCD摄像机，794 594像素，540线水平分辨率，最大光圈为F1．2时可拍摄最低照度为0．000 1 Lux，图像采集最大速率是30帧／s，摄像机镜头为手动光圈，焦距3．5～8 mm，视频采集卡采用NI公司PCI-1411。视频获取软件采用NI公司的IMAQ Vision模块，该模块具有图像采集、系统校准、图像处理、几何量测量、图像分割等众多子函数库，能够完成图像的去噪、增强、复原、分割、提取特征、灰度和二值图像处理及形状匹配、斑点分析、统计、滤波、几何变换、计算和测量等任务；视频处理软件采用G语言的虚拟仪器开发平台LabVIEW编写，主要采用数据流的驱动方式，编译后运行速度接近于C语言，并能驱动众多厂家的多种数据采集卡，具有强大的数据采集能力和信号处理功能，能够直观高效地表现编程算法。

2 光点检测原理
    点光源的安装位置和检测是建立完整精确运动模型的基础。模型建立精确性的核心问题是完成光点检测并使其具有较高的鲁棒性。
    由于检测的是红色LED，光斑的R分量占据优势，因此文中采用背景消减法，在读取背景帧和当前帧的过程中只需读取R分量，提高了运算效率。利用式(1)计算背景图像bk与当前帧图像fk的差分图像，从而检测出每帧图像中的运动目标区域
    Dk(x，y)=|fk(x，y)-bk-1(x，y)|      (1)
    其中，fk(x，y)和bk-1(x，y)分别为当前帧和背景帧R分量图像，Dk(x，y)为背景差分得到的R分量差分图像。
    检测出每一帧图像中的运动目标区域，克服了环境光场不稳定因素对检测结果的影响，提高了运动对象边缘的检测精度，为后续有效恢复连接肢体运动模型奠定基础。
    该光点检测方法，再通过对发光点特征参数的滤波、去噪，能够更加准确地识别发光点位置，进而通过精确的坐标系定位，完成对肢体运动过程的测量，为肢体运动模型的参数获取及肢体特征参数的测量提供了完整的实现依据。

3 肢体运动模型的连接恢复与数学模型建立
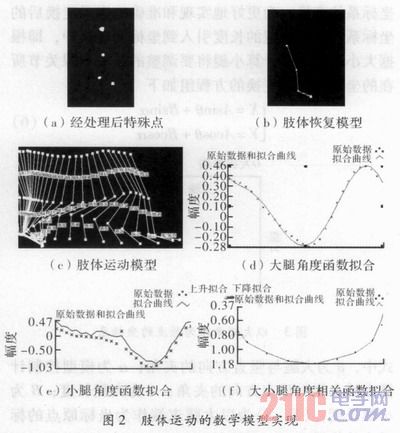
    光点检测获取的分割图，能够完整地识别与提取出安装在肢体各个节点的发光点，如图2(a)所示。应用LabVIEW标注出各个光点的坐标，采用光点连接技术，将每一帧图像上的4个发光点进行顺次逐一连接，即可获得代表脚掌、小腿、大腿的静态模型，如图2(b)所示。在每帧静态模型中通过对像素值的分析和对比，计算出每一像素值所代表的实际长度，进而换算出脚掌长度、小腿长度和大腿长度，这种视频测量的方法，要比实际测量的方法更为精确，为后续的模型分析提供了可靠数据。同时通过对连接成的模型相对于竖直位置的角度测量，能够测出脚掌、小腿、大腿相对于竖直方向的角度变化关系，记录各个相邻帧的模型相对竖直角度关系与时间的对应坐标如图2(c)所示，即可获得各个角度与时间的函数拟合图，如图2(d)和图2(f)所示。再根据大小腿角度变化与时间的关系，可计算出大小腿角度之间的函数关系如图3(e)所示这样即可得出3个代表性的模型如式(2)～式(5)所示。

[1] [2]  下一页